有机化学中的一些计数问题

0. 前言

今天（2025.10.10）上“行星有机化学”课的时候在讲有机化学的基础知识，讲到同分异构体个数的时候回忆起自己高中学OI的时候一直没搞明白烷烃、烯烃之类的计数问题，记得当时用的是生成函数，然而没有完全理解。所以读博的时候准备补高中的坑。

btw，这一阵学的各种东西都是在补之前不好好学习的坑……

参考资料1

upd on 2025.10.11 烷基计数O(n^3)完成

1. 烷基计数

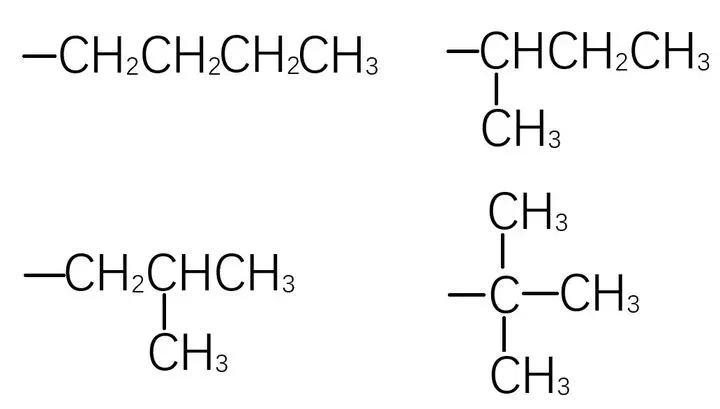
$n$ 个碳原子的烷基共有多少种同分异构体？（不考虑空间异构）

也就是说，是一个$n$个点每个点度数不超过4且根的度数不超过3的有根树的数目。

A. $\mathrm{O(n^3)}$

题目连接（LOJ6185）

DP，$f_i$是$i$个碳的烷基数，把根去掉之后就是把剩下的$i-1$ 个碳分给三个子树：$(j,k,i-1-j-k)$

然而我们怎么转移？

假设$\mathrm{get}(a,b,c)$ 表示我们计算三个子树分别为$(a,b,c)$的烷基答案

• 对于$a=b=c$的情况，$\mathrm{get}(a,b,c)=\binom{f_a}{3}+2\binom{f_a}{2}+\binom{f_a}{1}$
  • 这三项对应着选了三种（ABC）、选了两种（ABB、AAB）、只选一种（AAA）
  • 因为我们是可相等，但是也care顺序
  • 也可以这么理解，三个球+$f_a -1$个挡板，然后乱排有$\binom{f_a+2}{3}$个
• 对于$a=b\neq c$的情况，$\mathrm{get}(a,b,c)=\binom{f_a+1}{2}f_c$
• 对于$a\neq b$且$b\neq c$的情况，$\mathrm{get}(a,b,c)=f_a f_b f_c$

然后对应的$f_i=\sum\mathrm{get}(j,k,i-1-j-k)$

def alkyl_counts(N: int):
		f = [0] * (N + 1)
    f[0] = 1  # 空子树
    for i in range(1, N + 1):
        s = 0
        for a in range(0, i):
            for b in range(a, i - a):
                c = (i - 1) - a - b
                if b > c:
                    break
                fa, fb, fc = f[a], f[b], f[c]

                if a == b == c:
                    s = (s + C3(fa + 2)) % MOD
                elif a == b != c:
                    s = (s + C2(fa + 1) * fc) % MOD
                elif a < b == c:
                    s = (s + fa * C2(fb + 1)) % MOD
                else:  # 全不同
                    s = (s + fa * fb % MOD * fc) % MOD
        f[i] = s
    return f

retry