概率论与数理统计笔记
Feb 12, 2023··
2 min read
Boding Ouyang

0. 前言
这科更啥也不会,还考的贼早……快来补天吧,这科不补要挂。
1. 随机变量及其分布
1.1 离散型
- 0-1分布/伯努利分布:
- $P(X=1)=p$
- $P(X=0)=1-p$
- 二项分布:
- 一次试验发生概率$p$。把试验重复$n$次。$X$为发生的次数。
- $P(X=k)={n\choose k}p^k(1-p)^{n-k}$
- $X \sim B(n,p)$
- 几何分布
- 直到第$k$次0-1试验成功。
- $P(X=k)=q^{k-1}p$
- $X \sim G(p)$
- 无记忆性:$P(\xi >m+n|\xi >m)=P(\xi >n)$
- Pascal分布(负二项分布)
- $X_r$第$r$次0-1成功发生时试验次数
- $P(X_r=k)={r-1 \choose k-1}p^r q^{k-r}$
- Poisson分布
- $P(X=k)=\frac{\lambda ^k}{k!}e^{-\lambda},\lambda>0$
- $X\sim P(\lambda)$
- $n$重伯努利试验,如果$np_n\rightarrow\lambda$,则当$n\rightarrow∞$,二项分布分布律趋向于Poisson分布律。
- 离散均匀分布
- $P(x=a_i)=\frac{1}{n}$
1.2 连续型
- 分布函数:从负无穷积到$x$
- 正态分布:
- $f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp\{-\frac{(x-\mu)^2}{2\sigma^2}\}$
- $X\sim N(\mu,\sigma^2)$
- 标准:$N(0,1)$,记$\Phi(x)$分布函数,$\phi(x)$密度函数
- $N(\mu,\sigma^2)$的分布函数$F(x)=\Phi(\frac{x-\mu}{\sigma})$
- 指数分布
- $X\sim Exp(\lambda)$
- $$f(x)=\begin{cases}\lambda e^{-\lambda x}& \text{x>0}\\0& \text{x≤0}\end{cases}$$
- $$F(x)=\begin{cases}1-e^{-\lambda x}& \text{x>0}\\0& \text{x≤0}\end{cases}$$
- 均匀分布
- $X\sim U[a,b]$
- $$f(x)=\begin{cases}\frac{1}{b-a}& \text{a≤x≤b}\\0& \text{其他}\end{cases}$$
1.3 其他
- 多维分布
- 多维随机变量$X=(X_1,\dots, X_n)$
- 概念啥的和一维的差不多轻松yy
- 均匀分布也差不多
- 二维正态分布:$N(a,b,\sigma_1^2,\sigma_2^2,\rho)$:
- $$f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}exp\{-\frac{1}{2(1-\rho^2)}[\frac{(x-a)^2}{\sigma_1^2}-2\rho\frac{(x-a)(y-b)}{\sigma_1\sigma_2}+\frac{(y-b)^2}{\sigma_2^2}]\}$$
- 边缘分布
- $(X_1,\dots, X_n)$ 取 $m$ 个就叫 $m$ 维边缘分布
- 二维正态分布中:
- $$f_X(x)=\int _{-∞}^{∞}f(x,y)dy=\frac{1}{\sqrt{2\pi}\sigma_1}exp\{-\frac{(x-a)^2}{2\sigma_1^2}\}$$
- $$f_Y(y)=\frac{1}{\sqrt{2\pi}\sigma_2}exp\{-\frac{(y-b)^2}{2\sigma_2^2}\}$$
- 随机变量函数的概率分布
- 离散型原理可用大脑yy
- 连续型密度变换公式:$X\rightarrow f(x),x \in(a,b)$。$y=g(x)$严格单调连续,反函数$x=h(y)$的导数存在且连续,则$Y=g(X)$概率密度函数:$p(y)=f(h(y))|h'(y)|$
- 也可以先求出来分布函数,然后再求个导搞出来密度函数
- 推广到多维情况$|h'(y)|$换成雅可比行列式
- $\chi^2$分布
- $X_1,\cdots ,X_n\sim N(0,1)$,$\sum\limits_i X_i^2$的分布。
- 有再生性。
- $X\sim \chi_n^2\rightarrow EX=n,Var(X)=2n$
- $f(x)=\frac{1}{2^{n/2}\Gamma(\frac{n}{2})} x^{\frac{n}{2}-1}e^{-\frac{x}{2}}$
- 再生性
- $X\sim B(n,p),Y\sim B(m,p)$,且$X,Y$独立,则$X+Y\sim B(n+m,p)$(二项分布再生性)
- $X\sim P(\lambda),Y\sim P(\mu)$,且$X,Y$独立,则$X+Y\sim P(\lambda+\mu)$(泊松分布再生性)
- $X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$,且$X,Y$独立,则$X+Y\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$
- $X\sim \chi_n^2,Y\sim \chi_m^2$,且$X,Y$独立,则$X+Y\sim \chi^2_{n+m}$
- Pascal分布也有(不常用)
- 加减乘除变换
- 加:$X,Y\sim f(x,y),X+Y\sim p(z)=\int_{-∞}^{∞}f(x,z-x)dx=\int_{-∞}^{∞}f(z-y,y)dy$
- 除:$p_{\frac{X}{Y}}(z)=\int_{-∞}^{∞}|t|f(zt,t)dt$
- $t$分布
- $X_1\sim N(0,1),X_2\sim \chi^2_n$,且$X_1,X_2$独立,$Y=\frac{X_1}{\sqrt{X_2/n}}\sim t_n$,称为自由度为 $n$ 的 $t$ 分布。
- $f_Y(y)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(x+\frac{y^2}{n})^{-\frac{n+1}{2}}$
- 关于原点对称,$\lim_{n\rightarrow∞}f_Y(y)=\phi(y)$
- $F$分布
- $X_1\sim \chi_n^2,X_2\sim \chi_m^2$,且$X_1,X_2$独立,$Y=\frac{X_1/n}{X_2/m}\sim F_{n,m}$,称为自由度为$n,m$的$F$分布。
- $f_Y(y)=\frac{\Gamma(\frac{n+m}{2})}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}n^{n/2}m^{m/2}y^{n/2-1}(ny+m)^{-(n+m)/2}$
- 极大极小值分布
- $X_{(n)}=max\{X_1,\dots,X_n\},X_{(1)}=min\{X_1,\dots,X_n\}$,易得考虑分布函数简单
- $F_{X_{(n)}}=P(X_{(n)}\leq x)=\prod\limits_{k=1}^n P(X_k\leq x)=\prod\limits_{k=1}^nF_k(x)$
- $F_{X_{(1)}}(x)=1-\prod\limits_{k=1}^n(1-F_k(x))$
2. 随机变量的数字特征
2.1 数学期望与中位数
- 数学期望
- 离散型不用写了
- 连续型注意先得$\int_{-∞}^{∞}|x|f(x)dx<∞$时,数学期望才能存在!
- $X\sim B(n,p),EX=np$
- $X\sim P(\lambda),EX=\lambda$
- $X\sim Exp(\lambda),EX=\frac{1}{\lambda}$
- $X\sim \chi^2_n,EX=n$
- $X\sim t_n,EX=0$
- 相加线性性,独立的话可相乘
- 条件期望
- $E(Y|X=x)=\begin{cases}\int_{-∞}^{∞}yf(y|x)dy\\ \sum a_ip_i\end{cases}$
- 全期望公式:$EX=E\{E[X|Y]\}$
- 若求$EY$,先求$h(x)=E(Y|X=x)$,再求$Eh(x)$即可。
- 中位数
- $P(X\leq m)\geq\frac{1}{2},P(X\geq m)\geq\frac{1}{2}$
- $p$ 分位数跟着定义:$P(X\leq \mu_p)\geq p,P(X\geq \mu_p)\geq 1-p$
2.2 方差,相关系数以及其他数字特征
- 方差
- $Var(X)=E(X-EX)^2=EX^2-(EX)^2=\sigma^2$
- $\forall c\in const,Var(X)\leq E(X-c)^2$等号成立当且仅当$c=EX$。
- $X,Y$独立,$Var(aX+bY)=a^2Var(X)+b^2Var(Y)$
- $X\sim B(n,p),Var(X)=np(1-p)$
- $X\sim P(\lambda),Var(X)=\lambda$
- $X\sim U[a,b],Var(X)=\frac{(b-a)^2}{12}$
- $X\sim Exp(\lambda),Var(X)=\frac{1}{\lambda^2}$
- $X\sim N(\mu,\sigma^2),Var(X)=\sigma^2$
- $X^*=\frac{X-EX}{\sqrt{Var(X)}}$,叫$X$的标准化随机变量,$EX^*=0,Var(X^*)=1$。用于消除单位带来的影响。
- 矩
- $r\in N^*,E[(X-c)^r]$称为$X$关于$c$的$r$阶矩。
- $c=0$:原点矩
- $c=EX$:中心矩
- $r\in N^*,E[(X-c)^r]$称为$X$关于$c$的$r$阶矩。
- 协方差
- 已知$Var(X+Y)=Var(X)+Var(Y)+2E(X-EX)(Y-EY)$,由此定义$Cov(X,Y)=E(X-EX)(Y-EY)$,反应$X,Y$相关性。
- $Cov(X,X)=Var(X)$
- $Cov(X,Y)=EXY-EX\cdot EY$,若独立,则$Cov(X,Y)=0$
- $Cov(A+B,X)=Cov(A,X)+Cov(B,X)$
- $X_1,\dots,X_n,\Sigma=(Cov(X_i,X_j))$,这叫协方差矩阵。
- $(X,Y)\sim N(a,b,\sigma_1^2,\sigma_2^2,\rho),\Sigma=\begin{pmatrix}\sigma_1^2&\rho\sigma_1\sigma_2\\ \rho\sigma_1\sigma_2&\sigma_2^2\end{pmatrix}$
- 相关系数
- $\rho_{X,Y}=\frac{Cov(X,Y)}{\sqrt{Var(X)}\cdot\sqrt{Var(Y)}}=Cov(X^*,Y^*)$,叫相关系数,等于$0$时,$X,Y$不相关。(还是为了避免单位影响)
- $(X,Y)\sim N(a,b,\sigma_1^2,\sigma_2^2,\rho)\rightarrow\rho_{X,Y}=\rho$
- $X,Y$独立,$\rho_{X,Y}=0$
- $|\rho_{X,Y}|\leq1$,取等号的时候当且仅当有线性关系,1 的话正相关,-1 的话负相关。
- 柯西不等式:$\xi, \eta$平方可积:$[E\xi\eta]^2\leq E\xi^2 E\eta^2$,取等当且仅当$P(\xi=t_0\eta)=1,t_0\in const$
- 推论:$\xi, \eta$平方可积:$Cov(\xi,\eta)\leq\sqrt{Var(\xi)}\cdot\sqrt{Var(\eta)}$,取等条件和上面一样
- 非退化$\xi, \eta$平方可积,以下四个命题等价:
- $\xi, \eta$不相关。
- $Cov(\xi,\eta)=0$
- $E\xi\eta=E\xi E\eta$
- $Var(\xi+\eta)=Var(\xi)+Var(\eta)$
- 相互独立一定不相关,不相关不一定独立。(判断“不相关且不独立”的时候先搞出来$Cov(X,Y)=0$,之后再用边缘分布$f(x,y)\neq f_X(x)\cdot f_Y(y)$)
3. 大数定律和中心极限定理
3.1 大数定律
- 若对$\forall \epsilon>0,\lim\limits_{n\rightarrow ∞}P(|\xi_n-\xi|\geq\epsilon)=0$,称随机变量序列$\{\xi_n\}$依概率收敛到随机变量$\xi$,记 $\xi_n \stackrel{p}{\rightarrow} \xi$
- $\{X_n\}$独立同分布,公共的期望$\mu$、方差$\sigma^2$:$\overline{X}=\frac{1}{n}\sum X_k\stackrel{p}{\rightarrow}\mu$。($\{X_n\}$服从大数定律)
- 切比雪夫不等式:$X$的方差存在则:$P(|X-EX|\geq\epsilon)\leq\frac{Var(X)}{\epsilon^2},\forall\epsilon>0$
- 可用来估计$X$与$EX$偏差,但是不太精确
3.2 中心极限定理
- $\{X_n\}$公共的期望$\mu$、方差$\sigma^2$。
- $\sum X_i$的标准化形式:$\frac{1}{\sqrt{n}\sigma}(X_1+\dots+X_n-n\mu)$
- 中心极限定理:$\forall x\in \mathbb{R}, \lim\limits_{n\rightarrow∞}F_n(x)=\Phi(x)$($F_n(x)$为标准化形式是分布函数)。
- 棣莫弗-拉普拉斯定理:把二项分布带入中心极限定理。(可用正态分布估计二项分布)
- 也就是二项分布时:
- $\lim\limits_{n\rightarrow∞}P(\frac{\sum X_i-np}{\sqrt{np(1-p)}}\leq x)=\Phi(x),\forall x\in \mathbb{R}$
- $\frac{X-np}{\sqrt{np(1-p)}}\sim N(0,1)$
- 也就是二项分布时:
4. 数理统计的基础与抽样分布
4.1 样本的两重性和简单随机样本
- 样本空间:样本$X=(X_1,\dots,X_n)$可能取值的全体称为样本空间,记为 $\mathscr{X}$
- 样本两重性:样本既可m_k看成具体的数,又可以看成随机变量或随机向量。
- 用大写表示随机变量或随机向量,用小写表示具体的观察值
- 简单随机样本:$F$中抽$X_1,\dots,X_n$,若相互独立且相同分布,则称之为简单随机样本。(联合分布、联合密度累乘即可)
- 统计推断:样本推断总体
- 分布形式已知,但有未知参数,推断这个参数叫参数统计推断
- 两种方法是:参数估计和假设检验
- 形式都不知道叫非参数统计推断
- 分布形式已知,但有未知参数,推断这个参数叫参数统计推断
4.2 统计量
- 统计量是样本的函数
- 只与样本有关,不与未知参数有关
- 常用统计量
- 样本均值:$\overline{X}=\frac{1}{n}\sum X_i$
- 样本方差:$S^2=\frac{1}{n-1}\sum(X_i-\overline{X})^2$
- 样本$k$阶原点矩:$a_k=\frac{1}{n}\sum X_i^k$
- 样本$k$阶中心矩:$m_k=\frac{1}{n}\sum(X_i-\overline{X})^k$
- 次序统计量:把样本排个序$X_{(1)},\dots,X_{(n)}$
- 样本中位数:$m_{\frac{1}{2}}=\begin{cases} X_{(\frac{n+1}{2})}& \text{n为奇数}\\ \frac{1}{2}[X_{(\frac{n}{2})}+X_{(\frac{n}{2}+1)}]& \text{n为偶数} \end{cases}$
- 极值:$X_{(1)},X_{(n)}$
- 经验分布函数:$F_n(x)=\frac{X_1,\dots,X_n\text{中≤x的个数}}{n}$
- 正态变量线性函数的分布
- $X_1,\dots,X_n\sim N(a,\sigma^2),T=\sum c_k X_k\sim N(a\sum c_k,\sigma^2\sum c_k^2)$
- $c_k=\frac{1}{n}$即$T=\overline{X}:\overline{X}\sim N(a,\frac{\sigma^2}{n})$
- $X_1,\dots,X_n\sim N(a,\sigma^2),T=\sum c_k X_k\sim N(a\sum c_k,\sigma^2\sum c_k^2)$
- 正态变量样本方差的分布
- $\frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1}$
- $\overline{X}$与$S^2$独立
- 几个重要推论
- $X_1,\dots, X_n$独立同分布$\sim N(a,\sigma^2)$,则:$T=\frac{\sqrt{n}(\overline X-a)}{S}\sim t_{n-1}$
- $X_1,\dots,X_n\sim N(a_1,\sigma^2)$对应$Y$于$N(a_2,\sigma^2)$,互相都独立,则:$T=\frac{(\overline X-\overline Y)-(a_1-a_2)}{S_{w}}\cdot\sqrt{\frac{mn}{m+n}}\sim t_{n+m-2}$($(n+m-2)S_w^2=(m-1)S_1^2+(n-1)S_2^2$)
- $X_1,\dots,X_n\sim N(a_1,\sigma_1^2)$对应$Y$于$N(a_2,\sigma_2^2)$,互相都独立,则:$F=\frac{S_1^2}{S_2^2}\cdot\frac{\sigma_2^2}{\sigma_1^2}\sim F_{m-1,n-1}$
- $X_1,\dots,X_n$服从指数分布:$f(x,\lambda)=\lambda e^{-\lambda x}I_{[x>0]}$,则:$2\lambda n \overline{X}=2\lambda \sum X_i\sim \chi^2_{2n}$
5. 参数估计
5.0 基本概念
- 参数估计问题:
- 总体:$X\sim f_{\theta}(x),f\text{形式已知},\theta=(\theta_1,\dots,\theta_k)$为未知参数
- 样本:$X_1,\dots,X_n$
- 利用样本对参数$θ$的作出估计或估计它们的某个已知函数$g(θ)$
- 点估计:点估计:用样本的函数$T(X_1,\dots,X_n)$去估计$g(θ)$
- 区间估计:用一个区间去估计$g(θ)$
5.1 点估计
- 概述:用$X_1,\dots,X_n$来估计$\theta$,需要引入统计量$\hat{\theta}=\hat{\theta}(X_1,\dots,X_n)$。带入样本的值算出$\hat{\theta}$作为$\theta$估计值。
- $\hat{\theta}$:估计量
- 矩估计方法
- 样本$k$阶矩:$a_k=\frac{1}{n}\sum X_i^k,m_k=\frac{1}{n}\sum(X_i-\overline{X})^k$
- 总体$k$阶矩:$\alpha_k=EX^k,\mu_k=E(X-EX)^2$
- 矩估计原理是用样本的估计总体的,假设未知参数$\theta=(\theta_1,\dots,\theta_k)$,方程组:
- $\begin{cases}\alpha_1=f_1(\theta_{1:k})\\ \qquad \vdots\\\alpha_k=f_k(\theta_{1:k})\end{cases}$
- 反解
- $\begin{cases}\theta_1=g_1(\alpha_{1:k})\\ \qquad \vdots\\\theta_k=g_k(\alpha_{1:k})\end{cases}$
- 再用样本矩代替即可
- 原则是尽量用低阶矩,特点是简单,但是不唯一
- 最大似然估计方法
- 设样本$X=(X_{1:n})$概率密度函数:$f_\theta(x)$($x$为样本$X$的观察值),给定$x$,$\hat{\theta}=\hat{\theta}(x)$满足:$L(\hat{\theta})=\max L(x;\theta)$,$\hat{\theta}$即为最大拟然估计值
- 一般情况:$L(x;\theta)=\prod f_\theta(x_i)$
- 判断的时候先取个对数,固定$x$再对$\theta$微分之类的即可
- 举个例子:$X_{1:n}, X\sim N(a,\sigma^2)$,求$a,\sigma^2$的最大拟然估计量
- 对数拟然函数:$l(a,\sigma^2)=c-\frac{1}{2\sigma^2}\sum (x_i-a)^2-\frac{n}{2}\log(\sigma^2)$
- $\begin{cases}\frac{\partial l(a,\sigma^2)}{\partial a}=0\\\frac{\partial l(a,\sigma^2)}{\partial \sigma^2}=0\end{cases}$
- 则:$\hat{a}=\overline{X},\hat{\sigma^2}=\frac{1}{n}\sum(X_i-\overline{X})^2$
- 点估计的优良准则
- 相合性:对估计量最基本的要求,矩估计满足,最大拟然一般条件下满足
- 无偏性:$E\hat{g}(X_{1:n})=g(\theta)$,称为无偏估计量
- 有效性:两个无偏估计量的方差小的更有效
- 渐近正态性:$n$很大,趋近于正态分布
5.2 区间估计
- 概述:除了点估计$\hat{\theta}$,还希望给出个范围,包含$\theta$真值的可信程度
- 置信区间:在给定的置信水平之下,去寻找精度高的区间。
- 枢轴变量法
- 过程:
- 找到$T$(一个良好的点估计)与$g(\theta)$有关
- 找出一个函数$S(T,g(\theta))$的分布与$\theta$无关($S$为枢轴变量)
- $\forall a
- 取分布$F$的$\frac{\alpha}{2},1-\frac{\alpha}{2}$分位数,则:$P(\omega_{1-\alpha/2}\leq S(T,g(\theta))\leq \omega_{\alpha/2})=1-\alpha$。这就是我们要求的置信区间
- 举例说明:$X_{1:n}\sim N(\mu,\sigma^2)$,求参数$\mu$,$\sigma^2$的$1−\alpha$置信区间。
- $\frac{\sqrt{n}(\overline{X}-\mu)}{S}\sim t_{n-1}$
- $\frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1}$
- 则最后的置信区间分别为:
- $[\overline X-\frac{1}{\sqrt{n}}St_{n-1}(\alpha/2),\overline{ X}+\frac{1}{\sqrt{n}}St_{n-1}(\alpha/2)]$
- $[\frac{(n-1)S^2}{\chi^2_{n-1}(\alpha/2)},\frac{(n-1)S^2}{\chi^2_{n-1}(1-\alpha/2)}]$
- 过程:
- 大样本法
- 利用极限分布,建立枢轴变量
- 枢轴变量法
- 置信界:
- 只对一边感兴趣的时候
- $P_{\theta}(\theta\leq \overline{\theta})\geq 1-\alpha$:置信上界
- $P_{\theta}(\theta\geq \underline{\theta})\geq 1-\alpha$:置信下界
6. 假设检验
6.0 推荐阅读资料
6.1 基本概念
- 假设检验问题就是研究如何根据抽样后获得的样本来检查抽样前 所作假设是否合理。
- 两类错误
- “实际上 $H_0$ 成立但是它被拒绝”为第 $I$ 类错误(弃真)
- “实际上 $H_0$ 不成立但是它没有被拒绝” 为第 $II$ 类错误(存伪)
- 只限制第一类错误的原则下的检验方法,称为显著性检验
- 给定允许犯第一类错误概率的最大值$\alpha$,选取$\tau$使得:$P_{H_0}(T<\tau)\leq\alpha$。称$\alpha$为显著性水平。
- $\beta(\theta)=P_{\theta}(H_0\text{被拒绝})$:检验的功效函数
- 问题流程
- 提出假设检验问题:$H_0:\theta\in \Theta_0\leftrightarrow H_1:\theta\in\Theta_1$。$H_0$为零假设或原假设,$H_1$为对立假设或备择假设。
- 参数估计构造检验统计量$T=T(X_{1:n})$。
- 根据对立假设构造检验的拒绝域$W=\{T(X_{1:n})\in A\}$,$A$为一个集合或者区间。拒绝域可取$\{T(X_{1:n}>\tau)\}$,此时称$\tau$为临界值。
- 任意$\theta\in\Theta_0$犯第一类错误概率小于等于显著性水平$\alpha$。
- 结合$T$在$H_0$下分布,定出$A$。
- 几种常见假设检验问题
- 简单假设:$\theta=\theta_0\leftrightarrow\theta=\theta_1$
- 双侧假设:$\theta=\theta_0\leftrightarrow\theta\neq\theta_0$
- 单侧假设:轻易yy出来一边
- 做题方法:
- 求出$\theta$较优的点估计$\hat{\theta}$
- 寻找统计量$T=t(X_{1:n})$,使得当$\theta=\theta_0$时,$T$分布已知,可以查表找到对应分位数
- 寻找对立假设$H_1$实际意义,找到拒绝域
- 零假设成立时,第一类错误概率小于显著性水平$\alpha$,这个临界值方程解出来,也就是确定了拒绝域
- 根据样本观测值,算出检验统计量的样本观测值,在拒绝域中可以拒绝零假设
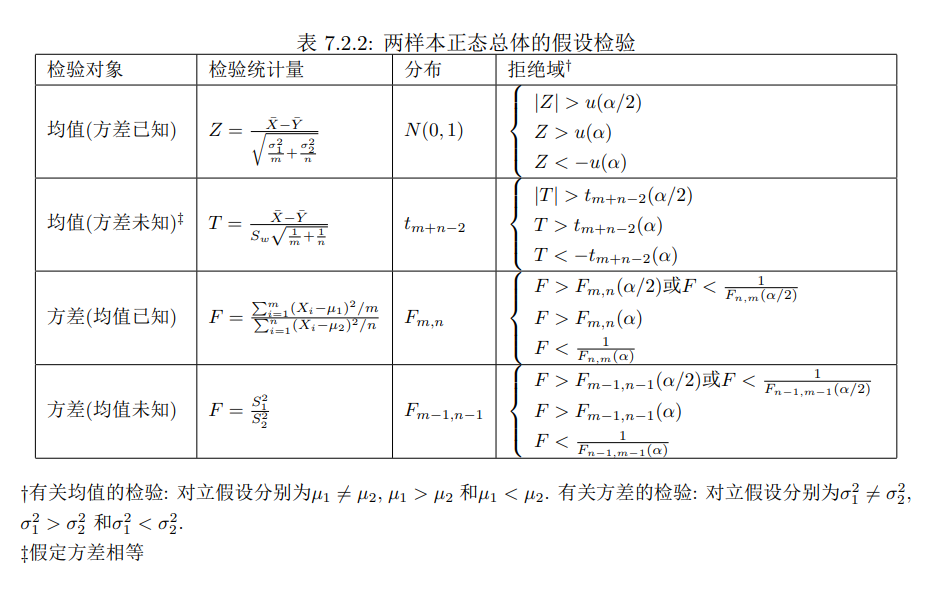
6.2 一样本和两样本总体参数检验
- 一样本正态总体参数检验
- 方差已知均值检验:
- 先考虑双侧假设($H_0:\mu=\mu_0\leftrightarrow H_1:\mu\neq\mu_0$)
- $\mu$极大拟然估计$\overline{X}$,标准化后的检验统计量$Z=\sqrt{n}\frac{\overline{X}-\mu_0}{\sigma}$
- yy出$H_0$成立的时候$|Z|$较小。所以拒绝域形如$\{|Z|>\tau\}$,所以$P_{H_0}(|Z|>\tau)=\alpha$
- 解得:$\tau=u_{\alpha/2}$,所以把观测值带入后找到拒绝条件
- 左右侧假设同理,这些被称为$Z$检验
- 方差未知时检验:
- 考虑检验:$H_0:\mu=\mu_0\leftrightarrow H_1:\mu\neq\mu_0$
- 由于方差未知,使用样本方差$S^2$代替总体方差$\sigma^2$得到检验统计量$T=\sqrt{n}\frac{\overline{X}-\mu_0}{S}$
- 在$H_0$下,$T\sim t_{n-1}$,所以拒绝域为$\{|T|>t_{n-1}(\alpha/2)\}$,这叫$t$检验
- 方差已知均值检验:
7. 做题的时候总结的杂碎重要知识点(和前面可能重合)
- $X\sim N(a,\sigma^2)$,则$EX^2=a^2+\sigma^2$
- $Var(cX)=c^2Var(x),Var(aX+bY)=a^2Var(x)+b^2Var(Y)$
- $X\sim N(\mu,\sigma^2)$,$\mu$的$1-\alpha$置信区间长度为$2St_{n-1}(\frac{\alpha}{2})/\sqrt{n}$
- $$\frac{\sqrt{n}(\overline{X}-\mu)}{S}\sim t_{n-1}$$
- $$\frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1}$$
- $X\sim Exp(x),EX=\frac{1}{\lambda},Var(X)=\frac{1}{\lambda^2}$
- $\overline{X}$(样本均值)与$S^2$(样本方差)独立
- $t$分布关于原点对称,$n$趋近于无穷的时候趋近于正态分布
- 假设检验中,在显著性水平$\alpha = 0.05$下若原假设$H_0$被接受,说明没有充分的理由表明$H_0$是错误的,因为如果落在拒绝域内,有足够理由$H_0$错误,不落在就取反!

8. 后记
先刷点题,后面的咕咕咕了
啊啊啊啊,概统咋就那么难啊,救命救命救命,我不想挂科!!!
希望这篇笔记保佑我概统能达到一个满意的分数吧,球球了啊啊啊啊啊!!!