立体角学习笔记

Sep 12, 2025·
Boding Ouyang
· 1 min read

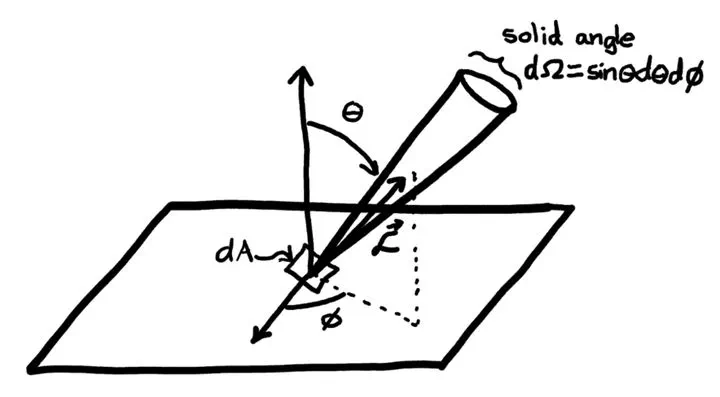
立体角（Solid Angle）

0. 前言

学到辐射传输的时候感觉自己的数理基础巨差（之前学过的都忘了）。。。特来补课。

参考资源1（应该是中央研究院的课的讲义注释）

参考资源2（丁峰老师的行星大气讲义）

参考资源3（维基百科）

1. 定义

描述文字

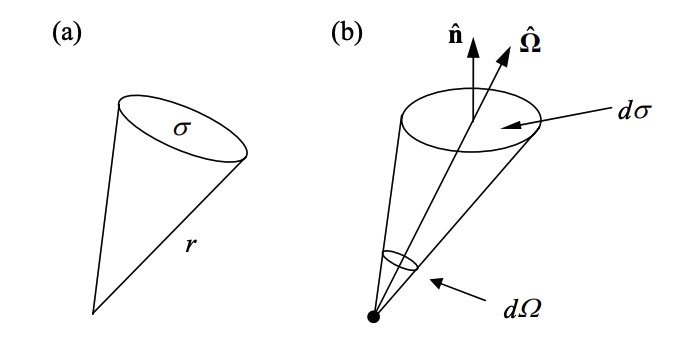
如图(a)，$\Omega=\frac{\sigma}{r^2}$，$\sigma$是这个锥体所截取的表面积

（全球立体角是$4\pi$，半球是$2\pi$，立体角的单位是$\mathrm{sr}$，steradian）

现在把立体角变得很小$d\Omega=\frac{d\sigma}{r^2}$，转化为球坐标$d\Omega=\sin\theta d\theta d\phi$

2. 应用

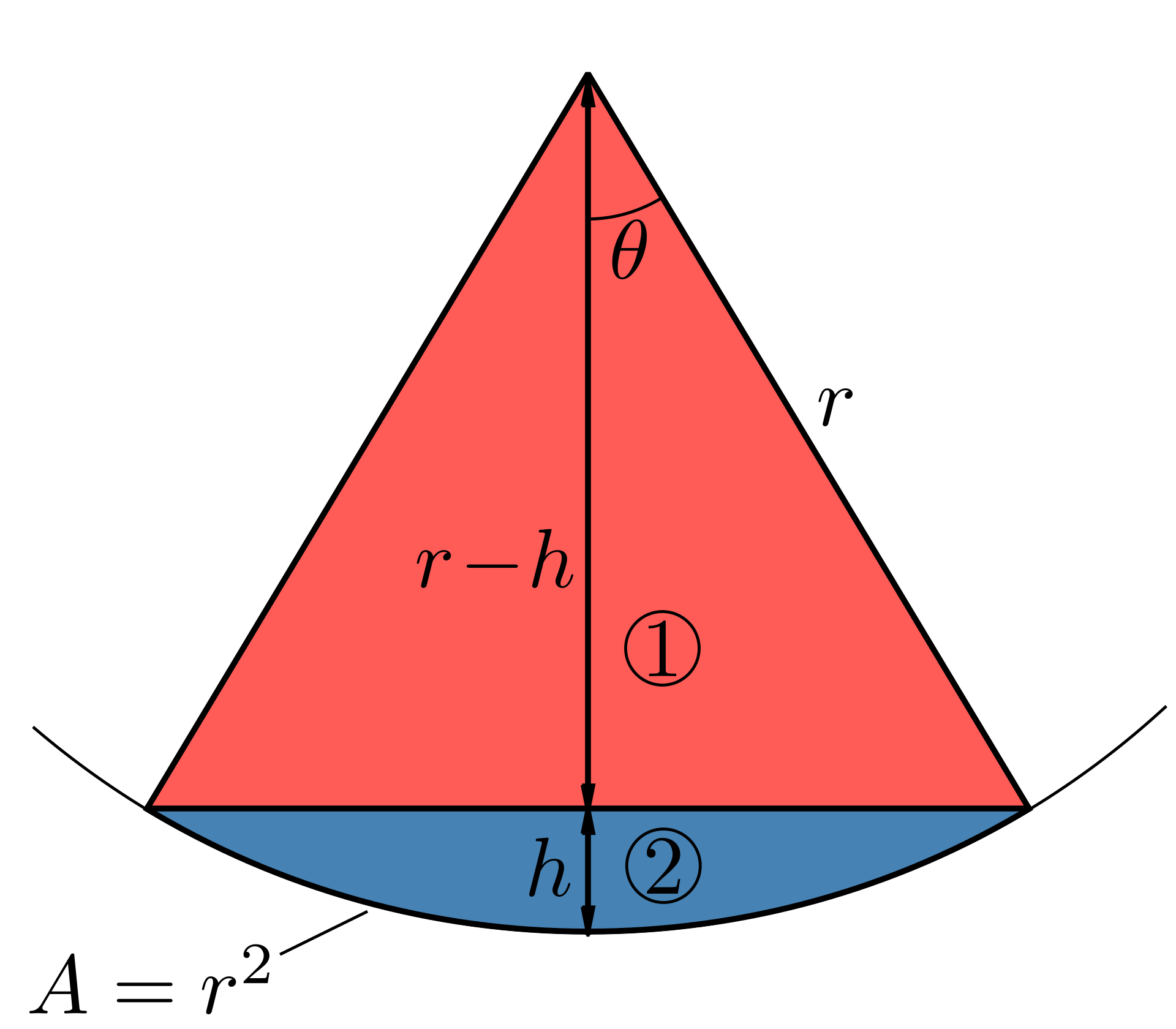
undefined

圆锥、球冠立体角（顶角为$2\theta$）：

  • $\int_0^{2\pi}\int_0^{\theta}\sin\theta'd\theta'd\phi=2\pi\int_0^{\theta}\sin\theta'd\theta'=2\pi(1-\cos\theta)$

计算太阳截面立体角：

  • 将太阳面积近似为表面积$\sigma$

  • $\Omega_\odot=\frac{\pi a_\odot^2}{d^2}$， （$1 \mathrm{AU}\approx 1.5 \times 10^{11} \mathrm{m} $， $a_\odot\approx 7\times 10^8\mathrm{m}$），所以$\Omega_\odot$很小

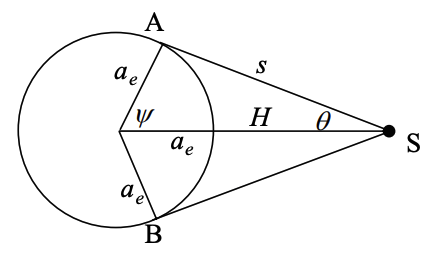
卫星绕地球运行，高度为$H$，立体角：

  • $\cos\theta=\frac{s}{a_e+H}$

  • $\Omega=2\pi(1-\cos\theta)$

3. 与辐射相关

辐射只有一个方向的极端情况：

  • 辐射强度（$I$）不能定义，辐射通量密度（$S$）可以定义（平行光束辐射）

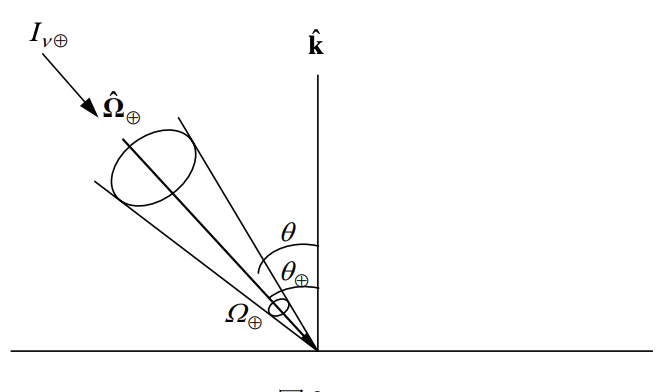
太阳辐射（太阳）：

  • $F_{\nu\odot}=\int_{\Omega_\odot}I_{\nu\odot}\cos\theta d\Omega=I_{\nu\odot}\cos\theta_\odot\int_{\Omega_\odot}d\Omega=\mu_\odot S_{\nu\odot}$

  • （$F_\nu=\int I_\nu \cos\theta d\Omega$，只取光线，定义部分的$\hat n, \hat \Omega$夹角）

  • 其中$\mu_\odot=\cos\theta_{\odot}, S_{\nu\odot}=I_{\nu\odot}\Omega_\odot$

  • $S_{\nu\odot}$：垂直太阳入射的面积元接收到的通量密度

  • $S_{\nu\odot}=I_{\nu\odot}\Omega_\odot=I_{\nu\odot}\frac{\pi a_\odot^2}{d^2}$

  • 然后对所有波数$\nu$ 积分就出来了常用的太阳常数$\bar S_\odot=1367\mathrm{W/m^2}$

  • 实际情况可设阳光为平行光度入射

如何计算望远镜接收到的恒星/行星的光子数：

  • 把恒星/行星看作一个发射盘（半径$R_*$，温度$T_*$）

  • $S_\nu=I_\nu \frac{\pi R_*^2}{d^2}=B_\nu(T_*)\frac{\pi R_*^2}{d^2}$

  • 望远镜收光面积$S$，望远镜观测时间$t$

  • 单位频率总能量：$S_\nu \ S \ t$

  • 除掉光子能量$h\nu$即可！

  • 所以接收到的光子数：$B_\nu(T_*)\frac{\pi R_*^2}{d^2}\frac{1}{h\nu}$

Mathematics Physics Notes